WebGL 三维模型的表示方式（三）

推荐使用NSDT 3DConvert进行3D模型格式转换，支持glb、obj、stp、fbx、ifc等多种3D模型格式之间进行互相转换，在转换过程中，能够很好的保留模型原有的颜色、材质等信息。

细分曲面

细分曲面通过为多边形网格附加一组可以使其更细化（利用细分）的规则以更好地近似所表示的曲面。在用这种方式解决离散近似产生的问题时，细分曲面与多边形网格具有相同的性能，这也促进了几何建模中细分方法的发展。细分成为曲线、曲面的离散和连续两种表示方式之间的桥梁。

Chaikin 算法

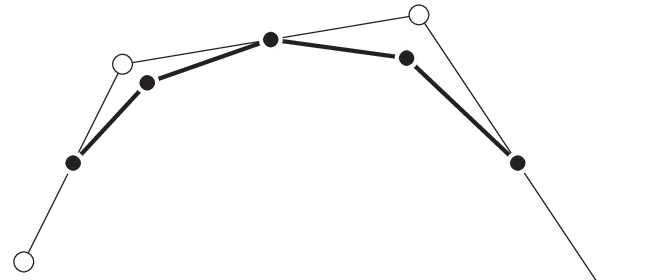
Chaikin 方法在特定情况下可以生成 二次B样条。与参数曲面一样，细分模式可以是插值或逼近方式。如果极限曲线是通过对初始控制多边形的点进行插值得到的，那么细分模式是插值方式。插值的每一个细分步骤都确保旧顶点和新生成顶点位于曲线上，并且旧顶点保留在原来的位置上。如果在每次细分后，旧顶点被丢弃或者根据某些规则进行移动，并不是对初始控制顶点进行插值而得到的曲线，那么该细分模式是逼近模式。综上，Chaikin 细分模式是逼近方式。

4点算法

4点算法是基于 插值模式 生成曲线的实例。这种细分模式使用顺序为 pi−2,pi−1​,pi​ 和 pi+1​ 的4个点相继生成新的点。细分规则如下图所示：

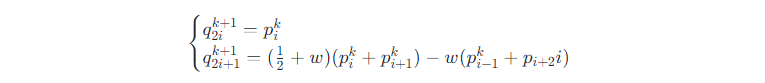
权重w使我们可以通过增加或减少曲线的张力来控制曲线的最终形状。当 w=0时，最终的曲线是初始点的线性插值曲线；当 w=1/16时，将得到一个三次插值曲线；当 0<w<1/8时，最终的曲线是连续可微的(C^1)。

细分方法分类

原始或对偶细分方式

如果一个细分模式是对网格的面进行细分，则称为 原始模式（面分割）；如果是通过顶点实现的，则成为 对偶模式（顶点分割）。

下图使用的 1-4 分割 是一种常用的原始细分模式，这种模式在保留旧顶点的同时，通过在较粗的网格的每一条边上插入一个新顶点，然后将新插入的顶点连接起来，而将一个面细分成4个新面：

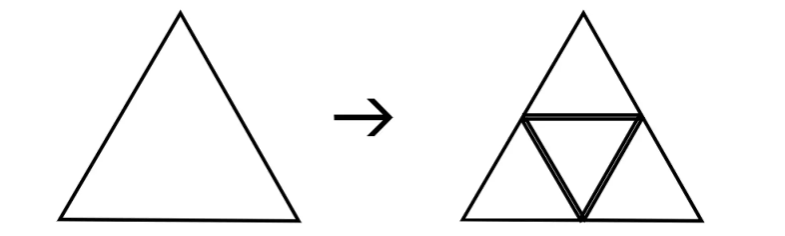
对偶细分模式针对多边形的对偶网格进行细分，将面的质心视为顶点，然后利用一条边将相邻面的新顶点连接起来。因此任一顶点的每个相邻面内部将生成一个新的顶点：

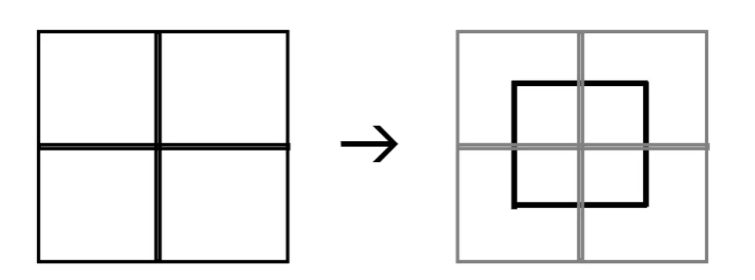
对于四边形网格，可以通过对偶细分得到仅包含四边形面片的细化网格；而对于三角形网格，顶点细分（对偶）模式将得到非嵌套六边形小面片。因此四边形非常特殊，能够自然地支持原始细分模式也支持对偶细分模式。

逼近与插值

细分方法可以通过对初始曲线和曲面进行插值，或者对初始控制网络进行逼近来生成曲线或曲面。原始模式既可以是插值的也可以是逼近的，而对偶模式本质上是逼近的。

插值在很多方面具有良好的特性：首先控制点也是极限曲面上的点；其次，可以显著地简化算法而提高计算效率；此外，针对不同的需要，可以通过在网格的不同部分执行不同的细分步数而将网格的细化进行局部调整。然而，插值模式生成的曲面质量低于逼近模式，并且收敛到极限曲面的速度通常也慢于逼近模式。

三维模型的表示方式就讲到这里了，总结共分成了3篇文章介绍，主要包括：

• 多边形网格
• 贝塞尔曲线/面和B样条曲线/面
• 曲面细分方式

对于表示方式还有很多方面，比如模型的数据结构、体素、几何建模、过程建模等。大家感兴趣可以继续去了解。