3D建模

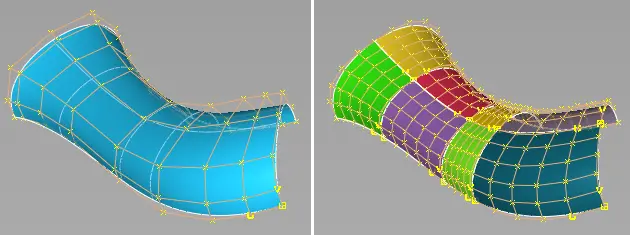
WebGL 三维模型的表示方式（二）

推荐使用NSDT 3DConvert进行3D模型格式转换，支持glb、obj、stp、fbx、ifc等多种3D模型格式之间进行互相转换，在转换过程中，能够很好的保留模型原有的颜色、材质等信息。

wangming

• 12 min read
WebGL 三维模型的表示方式（二）
推荐使用NSDT 3DConvert进行3D模型格式转换，支持glb、obj、stp、fbx、ifc等多种3D模型格式之间进行互相转换，在转换过程中，能够很好的保留模型原有的颜色、材质等信息。

在上篇文章中，我们介绍了多边形网格和隐式曲面，同时介绍了其优劣势。在本文，你将会听到熟悉的贝塞尔曲线、B样条曲线，同时我也会写示例以更加形象直观的向各位展示曲线。

参数曲线

在三维空间中，参数曲线定义为参数空间（

R

的子集）到三维空间

R^{3}

的映射：

C(t)=(X(t), Y(t), Z(t)) \qquad \tag{1}

其中

t

是曲线参数。通常，

t

的取值范围是

0 - 1

之间，曲线的起点为

C(0)

，终点为

C(1)

。

一般情况下，直接寻找

X(t)

、

Y(t)

和

Z(t)

的公式表达都是十分困难的。但是，存在利用曲线的直观性表示形式推导参数方程的方法。

可以把曲线表述为一个控制点序列，通过直接连接控制点可以得到分段曲线。此外还有更好的方法，通过引入一个调和函数基，能够以更平滑的方式连接控制点而获得一条平滑曲线。调和函数可以描述所有最终曲线或曲面的特征，例如：连续性和可微性，曲线或曲面是控制点的近似值还是插值等。

如果曲线经过所有的控制点，则得到 控制点插值曲线（如曲线

(a)

）；如果控制点只是引导线而不必位于曲线上，则得到 控制点近似曲线（如曲线

(b)

）。

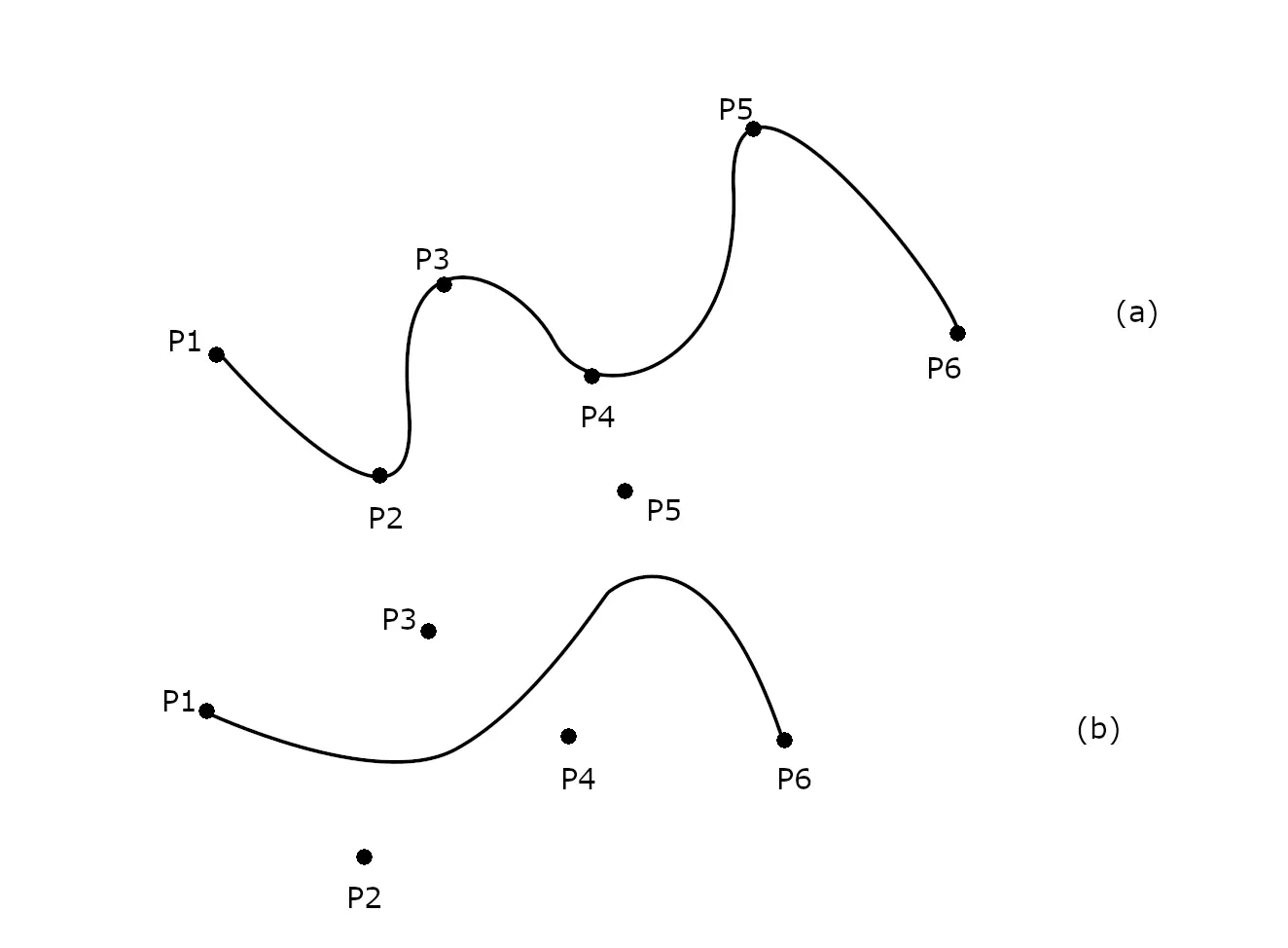
典型的参数曲线公式为：

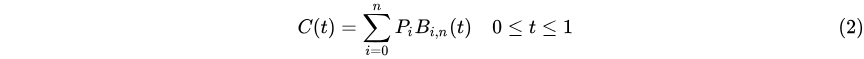
其中

P_{i}

是控制点，

\{B_i(\cdot)\}

是调和函数。控制点集合 也称为 控制多边形。

贝塞尔曲线

贝塞尔曲线 是计算机图形学中最常用到的参数曲线之一，起初是为了辅助汽车设计而开发的。贝塞尔曲线的数学定义如下所示：

P(t) = \sum_{i=0}^{n} P_{i}B_{i,n}(t) \qquad 0 \leq t \leq 1

其中

P_{i}

是控制点，

B_{i,n}(\cdot)

是

n

次 伯恩斯坦多项式。

n

次伯恩斯坦多项式的定义如下：

B_{i, n}(t) = \begin{pmatrix} n \\ i \end{pmatrix} t^{i} (1-t)^{n-i} \qquad i=0 \cdots n

其中，

\begin{pmatrix} n \\ i \end{pmatrix}

是二项式系数，即

\begin{pmatrix} n \\ i \end{pmatrix} = \frac{n!}{i!(n-i)!}

。下图分别展示了一次、二次、三次及四次伯恩斯坦多项式基：

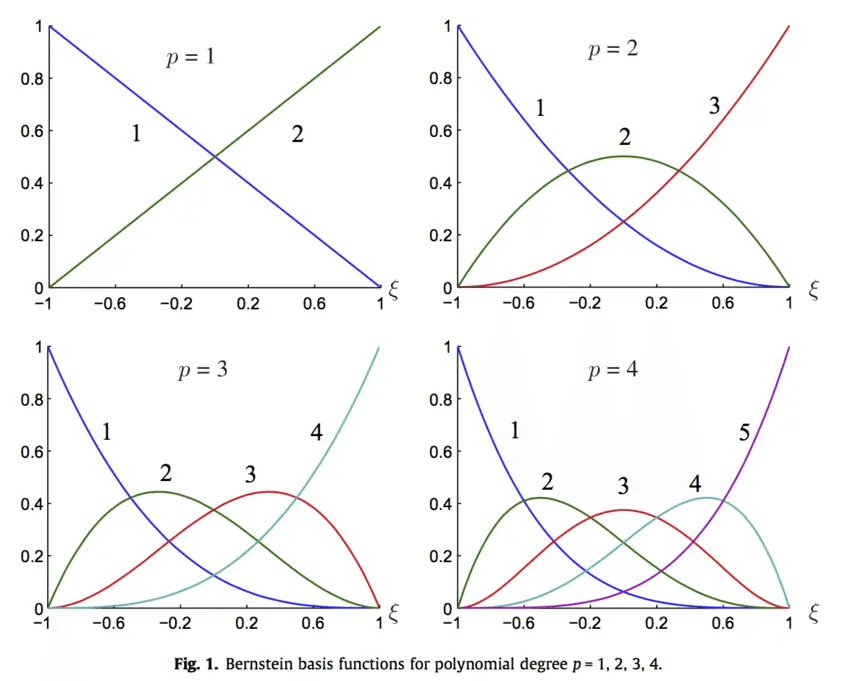
伯恩斯坦多项式广泛应用于参数曲线和曲面的调和函数，这是由于其具有以下特征：

n

次伯恩斯坦多项式集合

B_{n} = \{B_{0, n}(\cdot), B_{1, n}(\cdot), \cdots, B_{n, n}(\cdot)\}

构成了多项式向量空间的基；

B_{n}

是

B_{n-1}

的线性组合；

集合中多项式之和为1，即

\sum_{i=0}^{n} B_{i, n}(t)=1

。

我们可以来看一下antv中用到的数学库的贝兹插值的计算方式：

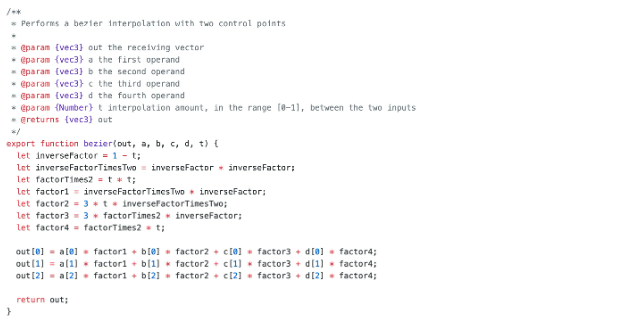
翻译成数学表达式如下：

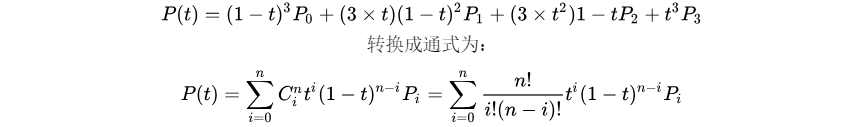
和我们的之前的描述的公式相同，没毛病！微软和苹果共同开发的TrueType字体就使用了以 贝兹样条 组成的二次贝兹曲线：

样条 是一种特殊的函数，由多项式分段定义。用低阶的样条插值能产生和高阶的多项式插值类似的效果。并且低阶的样条插值还具有“保凸”的重要性质。

下面我们使用antv中计算三次Bezier曲线插值的方法来看一下，当

t

从

0

变化到

1

时曲线的变化：

假如我们修改一下第二个控制点的位置，曲线又会变成什么样呢？

可以看到，虽然我们只修改了第二个控制点的值，但是后续曲线形状也跟随着发生了变化（下面也会在提到）。

B样条曲线

k

阶 B样条曲线 定义为：

P(t) = \sum_{i=0}^{n} P_{i}N_{i, k}(t)

，其中，

P_{i}

仍是控制点，

N_{i, k}(t)

是调和函数。当

k > 0

时，调和函数的递归定义如下：

N_{i, k}(t)=(\frac{t-t_{i}}{t_{i+k}-t_{i}})N_{i, k-1}(t) + \frac{t_{i+k+1}-t}{t_{i+k+1}-t_{i+1}}N_{i+1,k-1}(t) \tag{3}

对于

k=0

有：

N_{i,0}(t)=\begin{cases}1, \qquad t\in [t_{i}, t_{i+1}) \\ 0, \qquad 其它 \end{cases}

。

集合

\{t_{0},t_{1},\cdots,t_{n+k}\}

称为节点序列，且这个序列影响 B样条 的形状。如果节点序列是均匀的，即节点是等距的，那么 B样条 的定义变为

N_{i+1,k}(t)=N_{i,k}(t-t_{i})

，且调和函数沿着节点序列移动。均匀 B样条 调和函数

N_{i,k}(\cdot)

是区间

[t_{i}, t_{i+k})

上的

k

阶函数。

B样条曲线 的节点数决定了连接控制点的曲线的阶数，而不是 贝塞尔曲线 那样由控制点数目决定。这意味着 B样条曲线是局部的，节点值将影响曲线局部的形状；同时更重要的一个区别是，贝塞尔曲线必须经过起始和终止控制点。因此，相比 B样条曲线，贝塞尔曲线 在曲线段连接处进行平滑时更加困难。

基于以上原因，B样条曲线 通常比贝塞尔曲线更加灵活，但是

k

越大曲线对于控制点的支持就越有限。

下面三张图分别为由4个相同控制点控制的1阶、2阶和3阶B样条曲线，可以很明显的看出

k

的增加对控制点和曲线的影响：

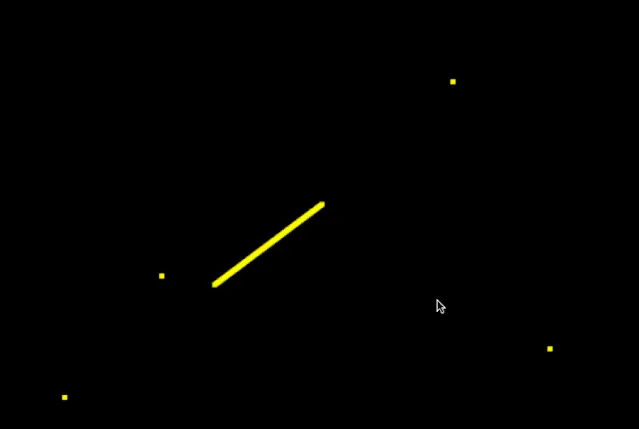
1阶B样条曲线

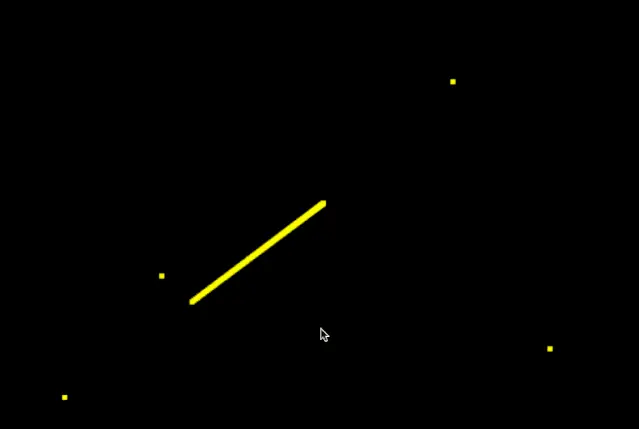
2阶B样条曲线

3阶B样条曲线

同时，当B样条是均匀的时候，对于给定的

n

，每个B样条基是其他基的平移拷贝而已。一个可以作为替代的非递归定义是：

N_{i,k}(t) = N_{n}(t + n - i), \qquad i=-1, ..., m+1

其中

N_{n}(t)=(m+1)\sum_{j=0}^{m+1}w_{j}(t_{j}-t)_{+}^{m}, \qquad t \in [0, 1] \\ w_{i}=\prod_{j=0,i \neq j}^{m+1} \frac{1}{t_{i} - t_{k}}
(t_{j} - t)_{+}

是截断幂函数。

贝塞尔曲面

参数曲线拓展为参数曲面是非常简单的。参数曲面的参数域是

R^{2}

的子集而不是

R

的，并且需要使用3个二元函数

(f:R^{2} \rightarrow R)

定义从参数到三维空间的映射：

S(u, v) = (X(u,v), Y(u,v), Z(u,v))

其中，

u

和

v

是曲面参数。通常，参数曲面的参数的取值范围也是从

0 - 1

。

对于参数曲线，可以将式

(1)

表示为式

(2)

所示的控制点和调和函数的线性组合。通过一些方法，可以将式

(2)

进行拓展以表示曲面。参数曲面最常用的形式之一是 张量积曲面，定义如下：

S(u, v) = \sum_{i=0}^{n} \sum_{j=0}^{m}P_{ij}B_{i}(u)B_{j}(v)

其中，

P_{ij}

是初始控制点，

B_i(\cdot)

和

B_j(\cdot)

是调和函数。此时，控制点

P_{ij}

称为曲面

S

的控制网络。由于参数

(u, v)

的取值域是

R^{2}

中的矩形，张量积曲面 也称为 矩形面片。

根据张量积曲面，贝塞尔曲线的定义可以拓展为如下曲面形式：

S(u, v)=\sum_{j=0}^{m} \sum_{i=0}^{n} P_{ij}B_{i}(u)B_{j}(v)

其中，

P_{ij}

是控制网络中的点，

B_{i,n}(\cdot)

是伯恩斯坦多项式，

B_{j,m}(\cdot)

是

m

阶伯恩斯坦多项式。

NURBS 曲面

非均匀有理B样条 是通过对 非有理B样条 使用的调和函数配比进行泛化的结果。泛化拓展了可被表示的曲线集合。贝塞尔曲线 的最终形式是多项式，而多项式无法表示圆锥形曲线，也就是锥体与平面的绞线（比如圆）。但是，多项式配比形式可以表示二次曲线，因此使用调和函数配比拓展了可被表示曲面的种类。非均匀 是指节点序列是不均匀的。k 阶 NURBS 曲线定义为：

P(t)=\frac{\sum_{i=0}^{n} w_{i}P_{i}N_{i,k}(t)}{\sum_{i=0}^{n} w_{i}N_{i,k}(t)}

，

n

是控制点的数目，

P_{i}

是控制点，

\{N_{i,k}(t)\}

是调和函数，调和函数

w_{i}

是用于调节曲线形状的权重，这与B样条曲线相同。

与贝塞尔曲面的拓展方式一样，可以通过张量积曲面将NURBS曲线拓展为NURBS曲面：

S(u,u)=\frac{\sum_{i=0}^{n} \sum_{j=0}^{m} w_{ij}P_{ij}N_{i,k}(u)N_{j,m}(v)}{\sum_{i=0}^{n} \sum_{j=0}^{m} w_{ij}N_{i,k}(u)N_{j,m}(v)}
NSDT场景编辑器 | NSDT 数字孪生 | GLTF在线编辑器 | 3D模型在线转换 | UnrealSynth虚幻合成数据生成器 | 3D模型自动纹理化工具
2023 power by nsdt©鄂ICP备2023000829号