WebGL 三维模型的表示方式（一）

推荐使用NSDT 3DConvert进行3D模型格式转换，支持glb、obj、stp、fbx、ifc等多种3D模型格式之间进行互相转换，在转换过程中，能够很好的保留模型原有的颜色、材质等信息。

三维模型

三维模型一般是指空间中物理实体对象的数学表示（以后遇到外行人问这个问题，又能用这个说法去装个13了，别细问，再问就不会了）。具体来讲，三维模型是由其形状和颜色外观的描述构成的。通常，三维对象的表示方法可以分为 面表示 和 体表示。

那么我们怎么能得到三维模型的数学表示呢？

除了我们熟知的使用 Maya、3D Max、Blender 等软件建模之外，也可以通过数字化技术测量实体对象从而获得其数字描述。其中 三角测量技术 最为著名，其主要思想是：对将要进行数字化的对象的表面投射特定模式的光，然后利用摄像机对表面的光反射过程进行拍摄。投影仪和摄像机的相对位置是已知的，因此可以推导出来光投射在表面上的每个点的位置。

同时还有 Kinect、飞行时间技术 等测量方式，再次就不赘述详细介绍。

多边形网格

从上图可以看出，一个多边形网格是利用多边形单元，如三角形、四边形等，对一个连续曲面的分割。更为形（装）式（13）化的描述为：网格

可以被定义为一个多元组

，其中

是模型的顶点集合（

中的点），

包含点之间的连接信息，即顶点如何连接以形成网格的边和面。例如，由一个三角形构成的网格可以表示为

，多元组中的元素分别代表三个顶点、三条边以及构成的三角形。

三角形扇和三角形带

在绘制三角形的文章中，有提到在 WebGL 中绘制有各种模式如点、三角形、三角形扇、三角形带等。接下来会介绍一下三角形扇与三角形带的应用。

一个顶点

的相邻顶点集合称为顶点的 1环，

的基数称为顶点

的 度 或 价。共享一个顶点的一组相邻三角形称为 三角形扇，而可以无歧义地通过枚举顶点进行说明的一组三角形称为 三角形带。

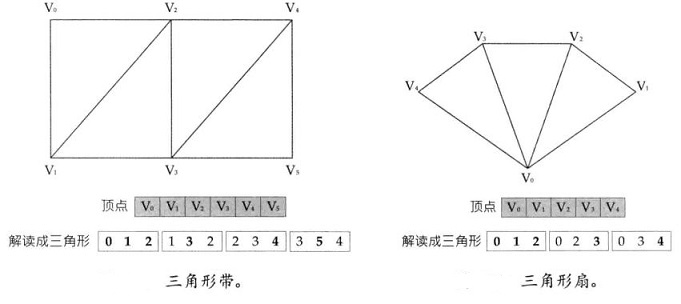
三角形带和三角形扇可以用于压缩物体的网格表示。

个顶点的三角形带可以表示

个三角形，因此100个三角形的三角形带需要储存102个顶点而不是300个。储存的顶点数目随着三角形数目的增加而增加，顶点的平均数

可以表示由

个三角形组成的三角形带中的一个三角形，计算形式为

。在三角形扇情况下，顶点有序列表

表示一个共享顶点

的三角形

，三角形扇与三角形带有相同的压缩性能，即 每个三角形的顶点平均数相同。

流形

如果表面上每一个相邻点与一个圆盘是 同胚 的，那么这个表面就是 二维流形 的。

首先来了解下面几个概念：

拓扑空间： 拓扑空间是一种数学结构，可以在上面形式化地定义出如收敛、联通、连续等概念。拓扑空间是一个集合

和其上定义的拓扑结构

组成的二元组

。

的元素

通常称为拓扑空间

的点。而拓扑结构

一词涵盖了开集、闭集、邻域、开核、闭包、导集、滤子等若干概念。从这些概念出发，可以给拓扑空间

作出若干种等价的定义。
欧几里得空间： 欧几里得空间是在约公元前300年，由古希腊数学家欧几里得建立的 角与空间中距离之间联系的法则。

连续函数： 连续 是函数的一种属性。直观上来说，连续的函数就是当输入值的变化足够小时，输出的变化也会随之足够小的函数。如果输入的某种微小的变化会产生输出值的一个突然的跳跃甚至无法定义，则这个函数是不连续的函数。

同构： 在抽象代数中，同构 指的是一个保持结构的双射。

在拓扑学中，同胚是两个拓扑空间之间的双连续函数。同胚 是拓扑空间范畴中的同构，也就是说，它们是保持给定空间的所有拓扑性质的映射。如果两个空间之间存在同胚，那么这两个空间就称为同胚的，从拓扑学的观点来看，两个空间是相同的。

大致地说，拓扑空间是一个集合物体，同胚就是把物体连续延展和弯曲，使其成为一个新的物体。因此正方形和圆是同胚的，但球面和环面就不是。有一个笑话是说，拓扑学家不能区分咖啡杯和甜甜圈，这是因为一个足够柔软的甜甜圈可以捏成咖啡杯的形状。

流形 是可以局部欧几里得空间化的一个拓扑空间，是欧几里得空间中的曲线、曲面等概念的推广。欧几里得空间就是最简单的流形的实例。地球表面这样的球面则是一个稍微复杂的例子。一般的流形可以通过把许多平直的片折弯并粘连而成。

流形 是普通表面的一个特征，多边形网格曲面可以通过检查一下条件是否成立而确定是否是流形：

• 边流形：每一边由一个（也就是该边处在网格边界上）或两个面共享；
• 顶点流形：如果两个面

和

共享一个顶点，那么遍历顶点的1环的边可以从

移动到

。换句话说，可以在不经过共享顶点本身的方式下遍历其所有的相邻点。

朝向

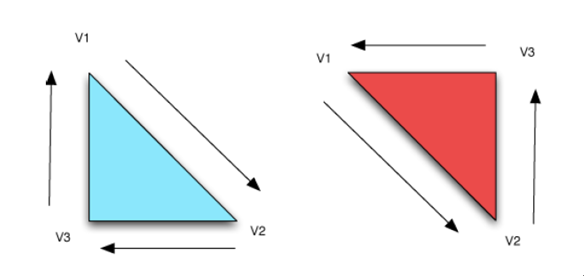
网格的每一个面片都是一个多边形，因此具有两面性。如果遵从在

中声明的顶点顺序来查看每一个表面，顶点将呈现出顺时针或逆时针的运动方向（如下图）。显然，如果从页面的后面看同一个多边形面片，顶点的运动方向则是恰好相反的。如果在两个面片

和

的每一条共享边上，顶点在面片的描述中顺序相反，那么

和

的朝向相同。

多边形网格的优劣

多边形网格有很多的局限性，因为网格是离散的表示，曲面只能通过组成网格的多边形平面进行分段近似，也就是说使用多边形平面越多，曲面的近似表示效果就越好。

另一个缺点是，网格表示不紧凑，高细节模型需要大量的数据进行表示。此外，多边形网格表示难以进行直接编辑，设计师不得不仔细修改表面的每一个元素，以获得所需效果。

尽管存在这些问题，计算机图形学领域仍致力于网格处理。重要原因之一是，相比于其他表现方式，多边形网格表示更为通用，即其他表示方式易于转换为多边形网格。并且，在屏幕上绘制三角形比绘制其他复杂的形状更为简单，而且易于优化。

隐式曲面

隐式曲面定义使给定三元函数

的函数值为0的点集

。在三维空间中，隐式曲面定义如下：

其中，

是笛卡尔直角坐标。集合

称为函数

的0集。例如半径为

的球体表面，可以表示为公式

，也可以变换为标准形式

。相比于平面或球体等基本几何图形，一个复杂的三维对象需要利用一组隐式表面函数表示，其中的每一个函数表示其表面的一部分。

代数曲面 是一类特殊的隐式曲面，其

是一个多项式。代数曲面的次数是多项式

各项中指数之和的最大值。二次曲面是集合建模中非常重要的一种曲面。二次曲面与每一平面相交，能够以适当或者退化方式形成17种标准曲面。例如，平行平面、椭球平面、椭圆锥面、椭圆柱面、抛物柱面、单叶双曲面、双叶双曲面都可以通过二次曲面与平面相交得到。