推荐：使用NSDT场景编辑器快速搭建3D应用场景

赋予动机

线性回归是机器学习中最基本的工具之一。它用于找到一条非常适合我们数据的直线。尽管它仅适用于简单的直线模式，但了解其背后的数学原理有助于我们理解梯度下降和损耗最小化方法。这些对于所有机器学习和深度学习任务中使用的更复杂的模型都很重要。

在本文中，我们将卷起袖子，使用 NumPy 从头开始构建线性回归。我们将从基础开始，而不是使用Scikit-Learn提供的抽象实现。

数据

我们使用Scikit-Learn方法生成一个虚拟数据集。我们现在只使用单个变量，但实现将是通用的，可以训练任意数量的特征。

Scikit-Learn提供的make_regression方法生成随机线性回归数据集，并添加高斯噪声以增加一些随机性。

X, y = datasets.make_regression(
        n_samples=500, n_features=1, noise=15, random_state=4)

我们生成 500 个随机值，每个值具有 1 个特征。因此，X 具有形状 （500， 1），并且 500 个独立 X 值中的每一个都有一个对应的 y 值。因此，y 也有形状 （500， ）。

可视化，数据集如下所示：

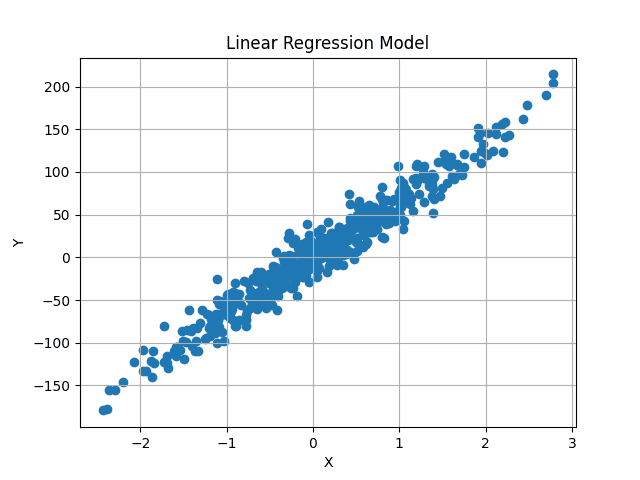
图片来源：作者

我们的目标是找到一条通过此数据中心的最佳拟合线，最大限度地减少预测值和原始 y 值之间的平均差异。

直觉

线性线的一般方程为：

y = m*X + b

X 是数字，单值。这里 m 和 b 表示梯度和 y 截距（或偏差）。这些是未知数，这些值的不同值可以生成不同的行。在机器学习中，X 依赖于数据，y 值也是如此。我们只能控制 m 和 b，它们充当我们的模型参数。我们的目标是找到这两个参数的最佳值，从而生成一条线，使预测值和实际 y 值之间的差异最小化。

这延伸到 X 是多维的场景。在这种情况下，m 值的数量将等于我们数据中的维度数量。例如，如果我们的数据有三个不同的特征，我们将有三个不同的 m 值，称为权重。

等式现在将变为：

y = w1*X1 + w2*X2 + w3*X3 + b

然后，这可以扩展到任意数量的要素。

但是我们如何知道我们的偏差和权重值的最佳值呢？好吧，我们没有。但是我们可以使用梯度下降迭代地找出它。我们从随机值开始，并在多个步骤中稍微更改它们，直到我们接近最佳值。

首先，让我们初始化线性回归，稍后我们将更详细地介绍优化过程。

初始化线性回归类

import numpy as np


class LinearRegression:
    def __init__(self, lr: int = 0.01, n_iters: int = 1000) -> None:
        self.lr = lr
        self.n_iters = n_iters
        self.weights = None
        self.bias = None

我们使用学习率和迭代次数超参数，这将在后面解释。权重和偏差设置为无，因为权重参数的数量取决于数据中的输入要素。我们还无法访问数据，因此我们暂时将它们初始化为“无”。

拟合方法

在 fit 方法中，我们获得了数据及其相关值。现在，我们可以使用这些来初始化权重，然后训练模型以找到最佳权重。

def fit(self, X, y):
        num_samples, num_features = X.shape     # X shape [N, f]
        self.weights = np.random.rand(num_features)  # W shape [f, 1]
        self.bias = 0

独立特征 X 将是形状 （num_samples， num_features） 的 NumPy 数组。在我们的例子中，X 的形状是 （500， 1）。数据中的每一行都有一个关联的目标值，因此 y 的形状也是 （500，） 或 （num_samples）。

我们提取它并随机初始化给定输入特征数量的权重。所以现在我们的权重也是一个大小为 （num_features， ） 的 NumPy 数组。偏差是初始化为零的单个值。

预测 Y 值

我们使用上面讨论的线方程来计算预测的 y 值。但是，我们可以遵循矢量化方法来加快计算速度，而不是对所有值求和的迭代方法。鉴于权重和 X 值是 NumPy 数组，我们可以使用矩阵乘法来获得预测。

X 具有形状（num_samples、num_features），粗细具有形状（num_features、）。我们希望预测的形状（num_samples，）与原始y值相匹配。因此，我们可以将 X 与权重相乘，或 （num_samples， num_features） x （num_features， ） 来获得形状 （num_samples， ） 的预测。

偏差值在每个预测的末尾添加。这可以简单地在一行中实现。

# y_pred shape should be N, 1
y_pred = np.dot(X, self.weights) + self.bias

然而，这些预测正确吗？显然不是。我们对权重和偏差使用随机初始化值，因此预测也将是随机的。

我们如何获得最佳值？梯度下降。

损失函数和梯度下降

现在我们有了预测值和目标 y 值，我们可以找到这两个值之间的差异。均方误差 （MSE） 用于比较实值数字。等式如下：

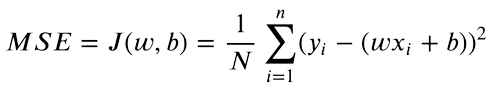
我们只关心我们价值观之间的绝对差异。高于原始值的预测与较低的预测一样糟糕。因此，我们将目标值和预测之间的差异平方，将负差异转换为正差异。此外，这会惩罚目标和预测之间的较大差异，因为更高的平方差异将导致最终损失。

为了使我们的预测尽可能接近原始目标，我们现在尝试最小化此函数。损失函数将是最小的，其中梯度为零。由于我们只能优化权重和偏置值，因此我们采用MSE函数相对于权重和偏置值的部分导数。

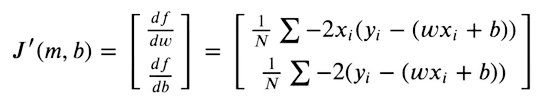
然后，我们使用梯度下降来优化给定梯度值的权重。

图片来自Sebasitan Raschka

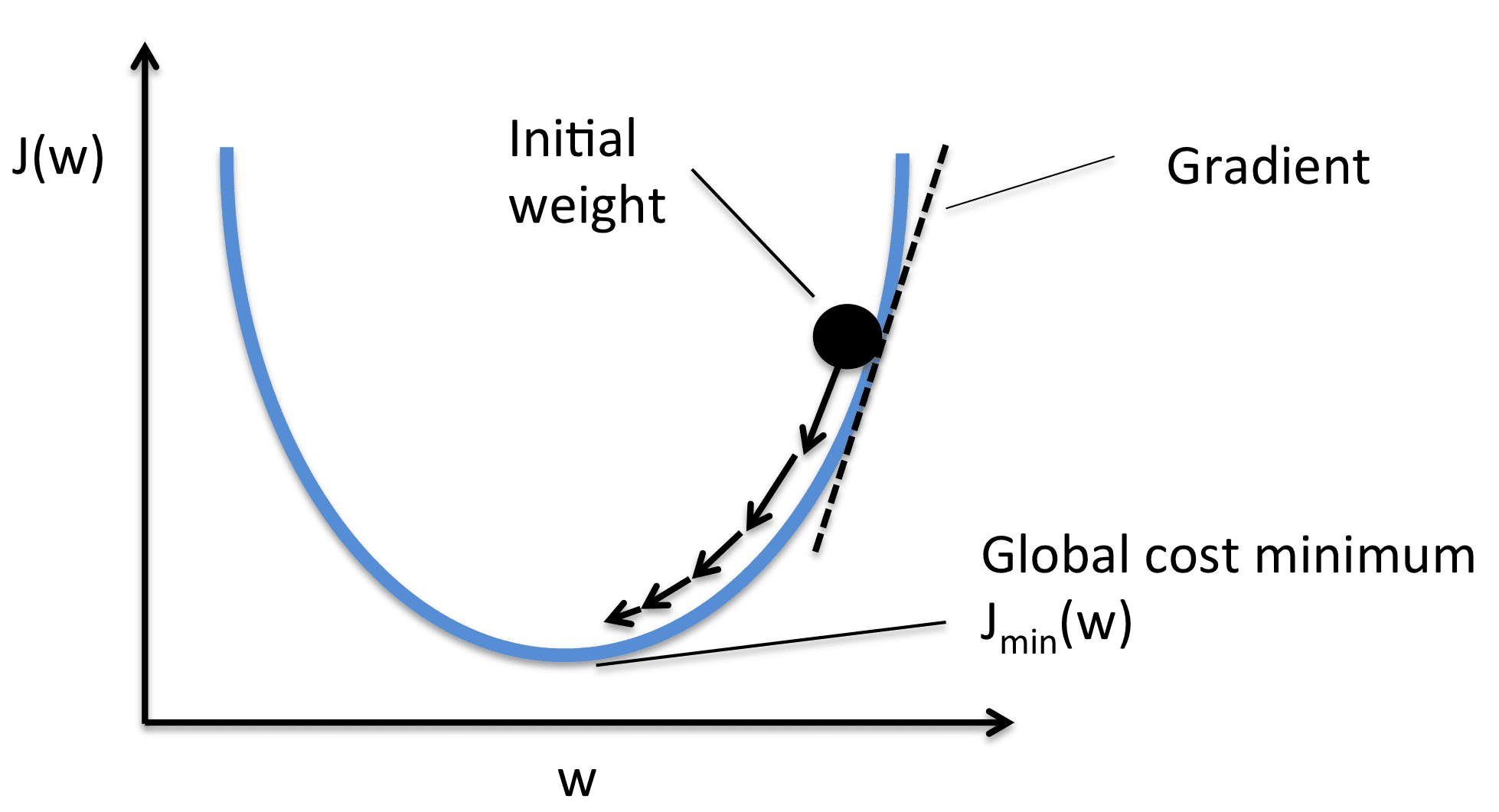
我们取每个权重值的梯度，然后将它们移动到与梯度相反的位置。这会将损失推向最小。根据图像，梯度是正的，因此我们减少了权重。这会将 J（W） 或损耗推向最小值。因此，优化方程如下所示：

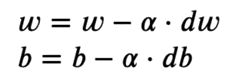
学习率（或阿尔法）控制图像中显示的增量步骤。我们只对值进行微小的更改，以稳定地向最小值移动。

实现

如果我们使用基本的代数操作来简化导数方程，这变得非常容易实现。

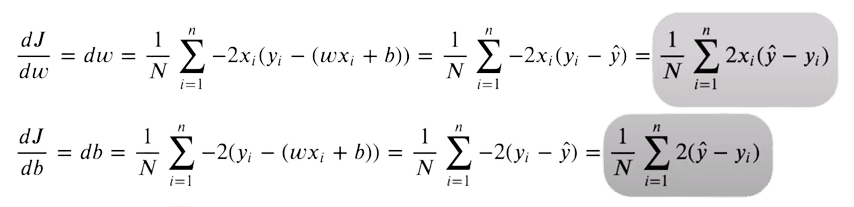
对于派生，我们使用两行代码实现这一点：

# X -> [ N, f ]
# y_pred -> [ N ]
# dw -> [ f ]
dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
db = (1 / num_samples) * np.sum(y_pred - y)

dw 的形状又是 （num_features， ） 所以我们对每个权重都有一个单独的导数值。我们分别优化它们。db 具有单个值。

为了优化现在的值，我们使用基本减法将值移动到与梯度相反的方向。

self.weights = self.weights - self.lr * dw
self.bias = self.bias - self.lr * db

同样，这只是一个步骤。我们只对随机初始化的值进行少量更改。我们现在反复执行相同的步骤，以收敛到最低限度。

完整循环如下：

for i in range(self.n_iters):

            # y_pred shape should be N, 1
            y_pred = np.dot(X, self.weights) + self.bias

            # X -> [N,f]
            # y_pred -> [N]
            # dw -> [f]
            dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
            db = (1 / num_samples) * np.sum(y_pred - y)

            self.weights = self.weights - self.lr * dw
            self.bias = self.bias - self.lr * db

预测

我们的预测方式与训练期间相同。但是，现在我们有了一组最佳的权重和偏差。预测值现在应接近原始值。

def predict(self, X):
        return np.dot(X, self.weights) + self.bias

结果

使用随机初始化的权重和偏差，我们的预测如下：

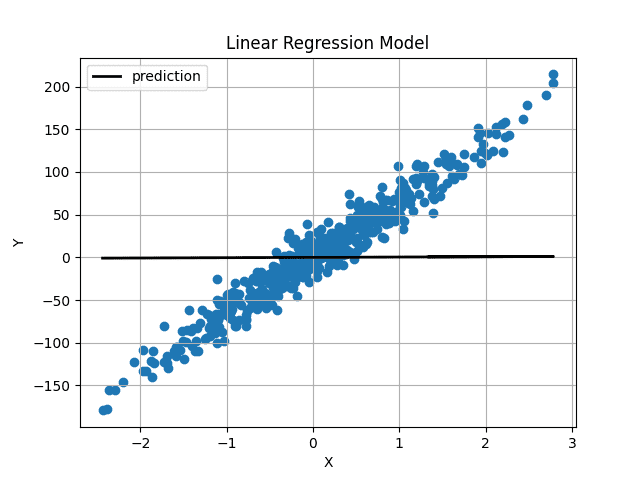
图片来源：作者

权重和偏差初始化非常接近 0，因此我们得到一条水平线。在训练模型 1000 次迭代后，我们得到：

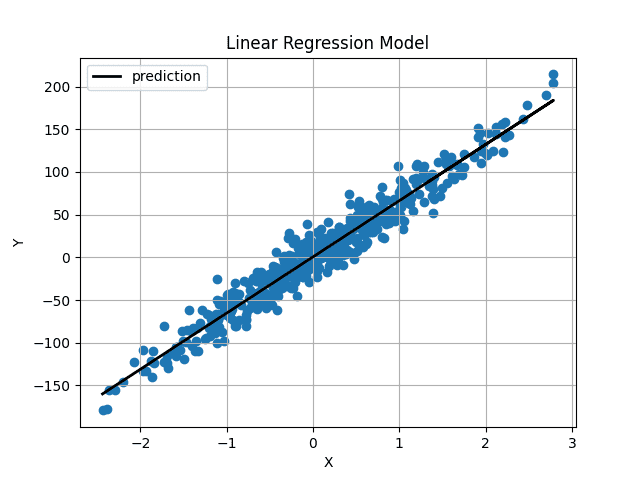
图片来源：作者

预测线直接穿过我们的数据中心，似乎是可能的最佳拟合线。

结论

您现在已经从头开始实现了线性回归。完整的代码也可以在GitHub上找到。

import numpy as np


class LinearRegression:
    def __init__(self, lr: int = 0.01, n_iters: int = 1000) -> None:
        self.lr = lr
        self.n_iters = n_iters
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        num_samples, num_features = X.shape     # X shape [N, f]
        self.weights = np.random.rand(num_features)  # W shape [f, 1]
        self.bias = 0

        for i in range(self.n_iters):

            # y_pred shape should be N, 1
            y_pred = np.dot(X, self.weights) + self.bias

            # X -> [N,f]
            # y_pred -> [N]
            # dw -> [f]
            dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
            db = (1 / num_samples) * np.sum(y_pred - y)

            self.weights = self.weights - self.lr * dw
            self.bias = self.bias - self.lr * db

        return self

    def predict(self, X):
        return np.dot(X, self.weights) + self.bias

Muhammad Arham是一名深度学习工程师，从事计算机视觉和自然语言处理工作。他致力于部署和优化几个生成式 AI 应用程序，这些应用程序在 Vyro.AI 年登上了全球排行榜。他对构建和优化智能系统的机器学习模型感兴趣，并相信持续改进。

由3D建模学习工作室 整理翻译，转载请注明出处！