WebGL入门-三角形的绘制

推荐使用NSDT 3DConvert进行3D模型格式转换，支持glb、obj、stp、fbx、ifc等多种3D模型格式之间进行互相转换，在转换过程中，能够很好的保留模型原有的颜色、材质等信息。

绘制多个点

在web-gl入门的最后有一个简单的绘画多个点的示例，但是这种只能画出最多一个点。当我们想要画多个有关联的点的时候，便不能使用。这时候就得使用缓冲区来一次存储多个点。具体步骤如下：

1. 创建缓冲区
2. 创建类型数组存储点位
3. 绑定缓冲区
4. 向缓冲区里填充数据
5. 向Attribute变量链接缓冲区
6. 容许Attribute变量使用缓冲区

具体代码如下：

const points = new Float32Array([ // 点位（x,y)
    0.5,  0.0, 
    0.0,  0.5, 
    -0.5, 0.0
]); 

const pointsBuffer = gl.createBuffer(); // 创建 buffer

gl.bindBuffer(gl.ARRAY_BUFFER, pointsBuffer); // 绑定 buffer 到 gl.array_buffer

gl.bufferData(gl.ARRAY_BUFFER, points, gl.STATIC_DRAW);

const pointsPosition = gl.getAttributeLocation(gl.program, 'pointsPosition');
gl.vertexAttribPointer(pointsPosition, 2, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(pointsPosition);

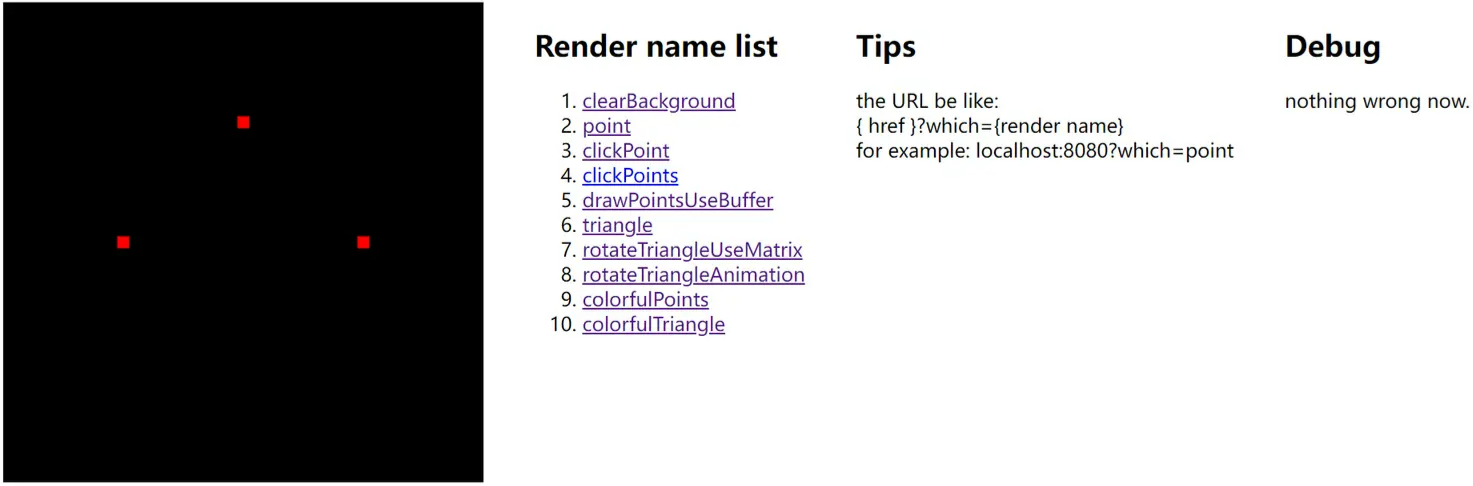
gl.drawArrays(gl.POINTS, 0, 3); // 从 第0个点开始画出 3个点

效果如下：

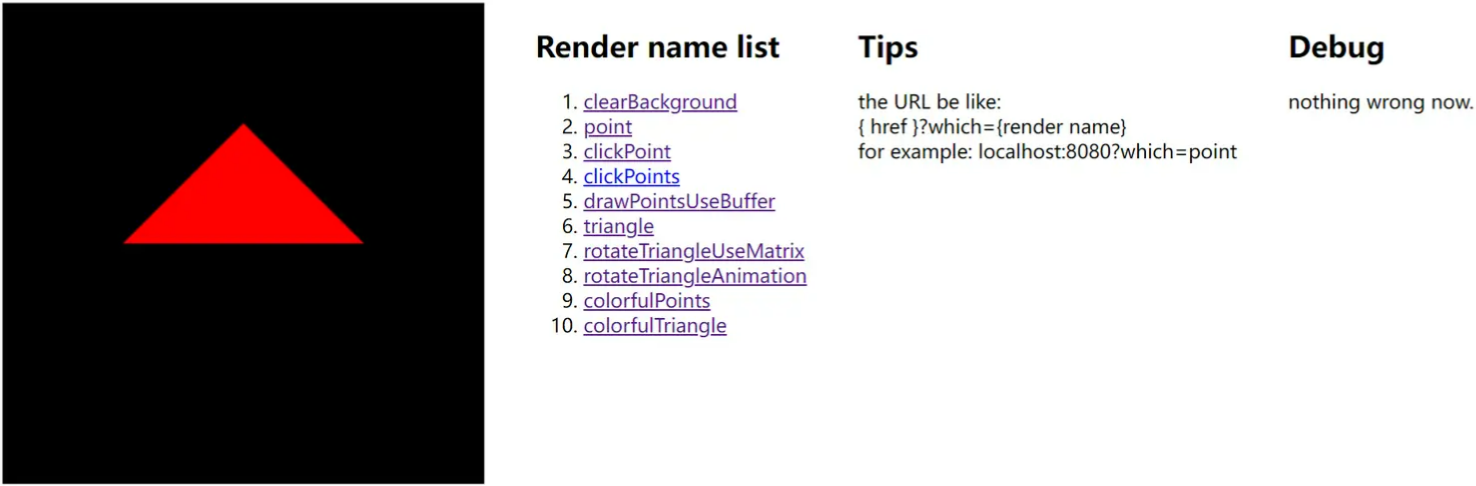
绘制三角形

将上面的程序中的gl.drawArrays(gl.points, 0, n); 改成 gl.drawArrays(gl.triangles, 0, n); ，再将顶点着色器里面的 gl_PointSize = 10.0 去掉就可以了。

gl.drawArrays(gl.triangles, 0, n);

效果如下：

这个API的第一个参数共有7种：

1. gl.POINTS 画点
2. gl.LINES 线段（v1, v2）, (v3, v4)
3. gl.LINE_STRIP 线段 （v1, v2), (v2, v3)
4. gl.LINE_LOOP 线段回路 （v1, v2) (v2, v3), (v3, v1)
5. gl.TRIANGLES 三角形
6. gl.TRIANGLE_STRIP 一系列三角形 （v1, v2, v3), (v2, v3, v4) ....
7. gl.TRIANGLE_FAN  扇区三角形 （v1, v2, v3), (v1, v3, v4) ....

移动、旋转、缩放（二维）

图形的二维层面移动依赖x, y坐标值的加减法。如公式所示：

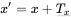
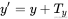
所以在顶点着色内部：

const pointsShader = `
    attribute vec4 PointsPosition;
    uniform vec4 Offset; // 由于是所有点都偏移，所以使用uniform
    void main() {
        gl_position = PointsPosition + Offset; // 点位矩阵相加直接产生偏移
    }
`;

旋转比较复杂，图形在坐标轴上的表示如图：

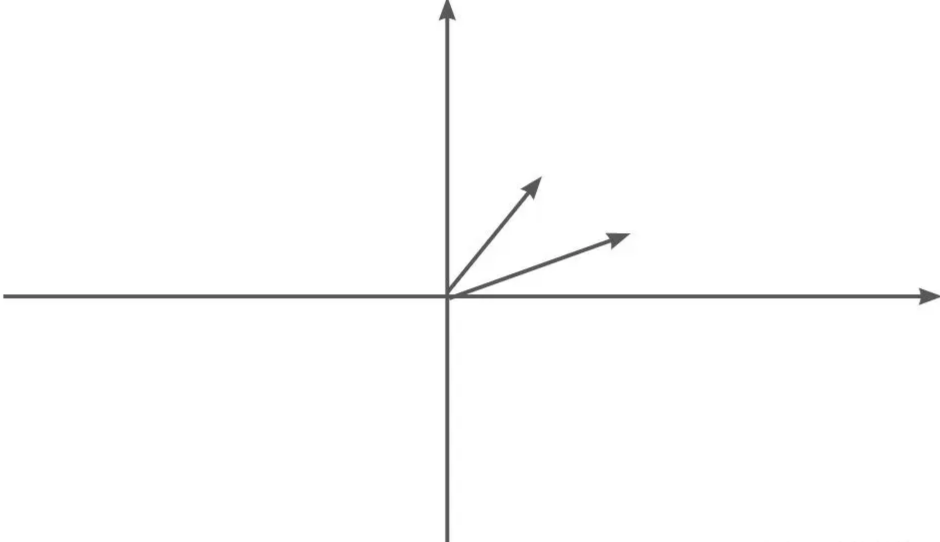
可以看到旋转的公式：

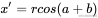
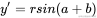
由三角函数两角和公式:

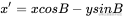
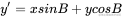
代码实现和平移一样只需要算出来即可。缩放就是乘法，不多赘述。

变换矩阵

通过矩阵乘法来简化公式，通过对比可以得知，(x', y', z') = [变换矩阵] * (x, y, z)，在变换图形时，只需要改变矩阵的值而不用重写计算公式，而且web-gl内置了矩阵计算工具，大大简化了复杂变化的计算难度。
比如通过上面的旋转公式可以倒推出旋转矩阵:

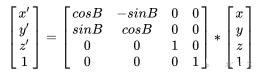
为了更形象，计算出x'的值：x' = consB * x + (-sinB) * y,就是上面的旋转公式。而当需要其他变换时，只需要更换矩阵，不用再编写新的公式大大简化复杂性。
编写代码的时候只需要：

const pointShader = `
    attribute vec4 PointsPosition;
    uniform mat4 OffsetMatrix; // 所有点通用
    void main() {
        gl_Position = PointsPosition * OffsetMatrix;
    }
`;
... // 片元着色器等

const angle = 60;
const radAngle = Math.PI * angle / 180.0;
const cosB = Math.cos(radAngle), sinB = Math.sin(radAngle);

const offsetMatrix = new Float32Array([
    cosB,  sinB, 0, 0,
    -sinB, cosB, 0, 0,
    0,     0,    1, 0,
    0,     0,    0, 1,
]); // 列主序

const offsetMatrixLocation = gl.getUniformLocation(gl.program, 'OffsetMatrix');
gl.uniformMatrix4fv(offsetMatrixLocation, 
                    false, /* 是否矩阵转置，web-gl不支持，所以为false */ 
                    offsetMatrix);

... // 绘制

最终效果：